| On the Number 55 | |
| 1) | On the Oracle: Heaven is one, earth is two; heaven is three, earth four; heaven is five, earth six; heaven is seven, earth eight; heaven is nine, earth ten. There are five heavenly numbers. There are also five earthly numbers. When they are distributed among the five places, each finds its complement. The sum of the heavenly numbers is 25, that of the earthly numbers is 30. The sum total of heavenly numbers and earthly numbers is 55. It is this which completes the changes and transformations and sets demons and gods in movement. — I Ching, Book II.9.1-2 (circa 1000 B.C.) Sum of 5 odd heavenly numbers = 1+3+5+7+9 = 25 Sum of 5 even earthly numbers = 2+4+6+8+10 = 30 Sum of the heavenly & earthly series (I Ching) = 25 + 30 = 55 |
| 2) | 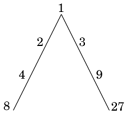 Platonic Lambda: The Soul of the Universe is the sum of the two series Platonic Lambda: The Soul of the Universe is the sum of the two series(Timaeus 35b): Sum of the double interval series (powers of 2) = 20 + 21 + 22 + 23 = 1 + 2 + 4 + 8 = 15 Sum of the triple interval series (powers of 3) = 30 + 31 + 32 + 33 = 1 + 3 + 9 + 27 = 40 Sum of the double & triple interval series (Timaeus) = 15 + 40 = 55 “Now God did not make the soul after the body, although we are speaking of them in this order; for having brought them together he would never have allowed that the elder should be ruled by the younger... First of all, he took away one part of the whole [1], and then he separated a second part which was double the first [2], and then he took away a third part which was half as much again as the second and three times as much as the first [3], and then he took a fourth part which was twice as much as the second [4], and a fifth part which was three times the third [9], and a sixth part which was eight times the first [8], and a seventh part which was twenty-seven times the first [27]. After this he filled up the double intervals [i.e. between 1, 2, 4, 8] and the triple [i.e. between 1, 3, 9, 27] cutting off yet other portions from the mixture and placing them in the intervals” (Benjamin Jowett's translation of Plato's Timaeus 35b) |
| 3) | In Pythagorean arithmetic, 2 is the first even number, 3 the first odd number. The even & odd tetractyes both radiate from the One, which is the source of all numbers. The sum of these two series is 55 |
| 4) | The 10th triangular number = 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 Sum of the first 10 numbers: 1+2+3+4+5+6+7+8+9+10 = 55 |
| 5) | Sum of the 2nd, 3rd, 4th, 5th, and 6th triangular numbers = 3 + 6 + 10 + 15 + 21 = 55 |
| 6) | The 10th Fibonacci number = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 (Leonardo Pisano Fibonacci, 1170-1250) |
| 7) | The 5th Pyramidal number = 1, 5, 14, 30, 55 |
| 8) | Sum of the first 5 square numbers = 1 + 4 + 9 + 16 + 25 = 55 |
Aristotle postulated a complex arrangement of 55
concentric spheres
with varying differential speeds,
all of them constructed of a transparent crystal of infinite purity and perfection.
(Charles-Albert Reichen, A History of Astronomy, Hawthorn, NY, 1961, p. 15)
“Since, then, the spheres involved in the movement of the planets themselves are—
eight for Saturn and Jupiter and twenty-five for the others, and of these only those
involved in the movement of the lowest-situated planet need not be counteracted the spheres
which counteract those of the outermost two planets will be six in number, and the spheres
which counteract those of the next four planets will be sixteen; therefore the number of all
the spheres— both those which move the planets and those which counteract these—
will be 55.”
to physical dimensions and visa versa


P = 16
T = 20
E = 5
N = 14
16+20+5+14 = 55 .. \ | / .. P+E+N+T = 55
55

The sides of the Tetractys have the values 1 2 3 4 9 8 27, which are called "the seven boundaries of all numbers" (Mead 164); arranged in this way they are called the Lambdoma or Platonic Lambda. Their significance is described below.
In addition to the Tetractys that increases by addition, 1 2 3 4, the Pythagoreans say there is another that increases by multiplication, that is, in geometric proportion. Plato (Tim. 31C) says that a continuous geometric proportion is the most perfect bond, and so we find such a proportion along both sides of the Lambdoma: 1 2 4 8 and 1 3 9 27.
The duple progression (1 2 4 8) represents "the evolution of the vehicle" proceeding out of Unity, that is, the differentiation and division that constitute the physical body. The triple progression (1 3 9 27), in the order of involution (27 9 3 1), represents "the development of consciousness" as a return to unity, that is, the unification and integration of the psyche. (Note that the Pythagoreans considered 1 to be neither even nor odd, nor even a number properly speaking, but the source of both the even and odd numbers; 2 was the first even and 3 the first odd.) In general, the duple axis represents the physical, temporal, divisible and perishable; the triple axis represents the incorporeal, eternal, indivisible and imperishable.
The Divine Proportion book relates this Golden Ratio to such things as the possible histories of energy level transitions of an electron in a hydrogen atom

http://en.wikipedia.org/wiki/Quantum_leap
Golden Ratio Discovered in Quantum World: Hidden Symmetry Observed for the First Time in Solid State Matter
ScienceDaily (Jan. 7, 2010) — Researchers from the Helmholtz-Zentrum Berlin für Materialien und Energie (HZB), in cooperation with colleagues from Oxford and Bristol Universities, as well as the Rutherford Appleton Laboratory, UK, have for the first time observed a nanoscale symmetry hidden in solid state matter. They have measured the signatures of a symmetry showing the same attributes as the golden ratio famous from art and architecture.
The research team is publishing these findings in the Jan. 8, 2010 issue of the journal Science.
On the atomic scale particles do not behave as we know it in the macro-atomic world. New properties emerge which are the result of an effect known as the Heisenberg's Uncertainty Principle. In order to study these nanoscale quantum effects the researchers have focused on the magnetic material cobalt niobate. It consists of linked magnetic atoms, which form chains just like a very thin bar magnet, but only one atom wide and are a useful model for describing ferromagnetism on the nanoscale in solid state matter.
When applying a magnetic field at right angles to an aligned spin the magnetic chain will transform into a new state called quantum critical, which can be thought of as a quantum version of a fractal pattern. Prof. Alan Tennant, the leader of the Berlin group, explains "The system reaches a quantum uncertain -- or a Schrödinger cat state. This is what we did in our experiments with cobalt niobate. We have tuned the system exactly in order to turn it quantum critical."
By tuning the system and artificially introducing more quantum uncertainty the researchers observed that the chain of atoms acts like a nanoscale guitar string. Dr. Radu Coldea from Oxford University, who is the principal author of the paper and drove the international project from its inception a decade ago until the present, explains: "Here the tension comes from the interaction between spins causing them to magnetically resonate. For these interactions we found a series (scale) of resonant notes: The first two notes show a perfect relationship with each other. Their frequencies (pitch) are in the ratio of 1.618…, which is the golden ratio famous from art and architecture." Radu Coldea is convinced that this is no coincidence. "It reflects a beautiful property of the quantum system -- a hidden symmetry. Actually quite a special one called E8 by mathematicians, and this is its first observation in a material," he explains.
The observed resonant states in cobalt niobate are a dramatic laboratory illustration of the way in which mathematical theories developed for particle physics may find application in nanoscale science and ultimately in future technology. Prof. Tennant remarks on the perfect harmony found in quantum uncertainty instead of disorder. "Such discoveries are leading physicists to speculate that the quantum, atomic scale world may have its own underlying order. Similar surprises may await researchers in other materials in the quantum critical state."
The researchers achieved these results by using a special probe -- neutron scattering. It allows physicists to see the actual atomic scale vibrations of a system. Dr. Elisa Wheeler, who has worked at both Oxford University and Berlin on the project, explains "using neutron scattering gives us unrivalled insight into how different the quantum world can be from the every day."
However, "the conflicting difficulties of a highly complex neutron experiment integrated with low temperature equipment and precision high field apparatus make this a very challenging undertaking indeed." In order to achieve success "in such challenging experiments under extreme conditions" the HZB in Berlin has brought together world leaders in this field. By combining the special expertise in Berlin whilst taking advantage of the pulsed neutrons at ISIS, near Oxford, permitted a perfect combination of measurements to be made.
The regular pentagon and the irrationality of the golden ratio
 | The golden ratio is the number  |
Note that if x and z are both multiples of y, then x-z is also a multiple of y.
Important fact. If x and y are non-zero numbers with x/y rational, then x and y are both multiples of some number r. That is, there is a number r and integers p and q such that x=pr and y=qr.
Proof of this fact. Observe that as x/y is rational, there are integers p, q such that x/y=p/q, and p and q are non-zero. Then x/p=y/q, and put r=x/p=y/q. Then, r is non-zero, x=pr and y=qr. That is, both x and y are multiples of r.
 | Consider the regular pentagon in Figure 2, together with the diagonal BE. Note that BE is parallel to CD. In Figure 2, assume that the fraction BE/ CD is rational. Then, using the fact above, there is a number r such that : BE is a multiple of r , and CD is a multiple of r. |
 | In Figure 3, BCDY is a parallelogram. So, CD=BY. As CD is a multiple of r, BY is a multiple of r. So, BY and BE are multiples of r, so EY is a multiple of r, because EY=BE-BY. But EY and BX are equal, and so EY and BX are multiples of r. Hence, BE, BX and EY are multiples of r. Because XY=BE-BX-EY, we nowhave: XY is a multiple of r, and BX is a multiple of r. |
 | In Figure 4, BPRX is a parallelogram. So, BX=PR. As BX is a multiple of r, from above, PRis a multiple of r. We now have: XY is a multiple of r, and PR is a multiple of r. |
 | To arrive at Figure 5, we used the regular pentagon ABCDE to construct the smaller regular pentagon XPQRY as n Figure 4. We have seen above that if BE and CD are multiples of r, then PR and XY are also multiples of r. This argument and construction can now be repeated, so that : when we obtain the new pentagon from the old one, both the sides and the diagonals of this new pentagon are also multiples of r. |
 | Figure 6 illustrates the first few regular pentagons in an infinite sequence of pentagons, each one constructed from the preceding one as described above. The above argument shows that all the sides and diagonals of all pentagons in the sequence are multiples of r. Thus, each side of each pentagon in the sequence of pentagons has a length that is at least r. But, this is impossible, because the pentagons are decreasing by a fixed ratio in size at each stage and eventually one of them will have a side of length less than r . Thus, if we assume that the ratio of the length of the diagonal of a regular pentagon to the length of the side of a regular pentagon is a rational number, we are led to a situation that is impossible. Our conclusion is: The assumption that the ratio is rational is incorrect. So, the ratio of the length of a diagonal of a regular pentagon to the side of the pentagon is irrational. |
When they said REPENT REPENT
I wonder what they meant
When they said REPENT REPENT
I wonder what they meant
When they said REPENT REPENT
I wonder what they meant
When they said REPENT REPENT ...
John 1:36 - "Behold, the Lamb of God who takes away the sin of the world!

Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry
Quantum phase transitions take place between distinct phases of matter at zero temperature. Near the transition point, exotic quantum symmetries can emerge that govern the excitation spectrum of the system. A symmetry described by the E8 Lie group with a spectrum of eight particles was long predicted to appear near the critical point of an Ising chain. We realize this system experimentally by using strong transverse magnetic fields to tune the quasi–one-dimensional Ising ferromagnet CoNb2O6 (cobalt niobate) through its critical point. Spin excitations are observed to change character from pairs of kinks in the ordered phase to spin-flips in the paramagnetic phase. Just below the critical field, the spin dynamics shows a fine structure with two sharp modes at low energies, in a ratio that approaches the golden mean predicted for the first two meson particles of the E8 spectrum. Our results demonstrate the power of symmetry to describe complex quantum behaviors.
"The group of symmetries of this strange geometry called E8 is one of the most intriguing structures that Nature has left for the mathematician to play with," commened Prof Marcus du Sautoy of Oxford University, currently in Auckland. "Most of the time mathematical objects fit into nice patterns that we can order and classify. But this one just sits there like a huge Everest."
What makes this group of symmetries so exciting is that Nature also seems to have embedded it at the heart of many bits of physics. One interpretation of why we have such a quirky list of fundamental particles is because they all result from different facets of the strange symmetries of E8. I find it rather extraordinary that of all the symmetries that mathematician’s have discovered, it is this exotic exceptional object that Nature has used to build the fabric of the universe. The symmetries are so intricate and complex that today’s announcement of the complete mapping of E8 is a significant moment in our exploration of symmetry."
For the feat, the team used a mix of theoretical mathematics and intricate computer programming to successfully map E8, (pronounced "E eight") which is an example of a Lie (pronounced "Lee") group. Lie groups were invented by the 19th century Norwegian mathematician Sophus Lie to study symmetry.
Underlying any symmetrical object, such as a sphere, is a Lie group. Balls, cylinders or cones are familiar examples of symmetric three-dimensional objects. Today’s feat rests on the drive by mathematicians to study symmetries in higher dimensions. E8 is the symmetries of a geometric object that is 57-dimensional. E8 itself is 248-dimensional.
"E8 was discovered over a century ago, in 1887, and until now, no one thought the structure could ever be understood," said Prof Jeffrey Adams, Project Leader, at the University of Maryland. "This groundbreaking achievement is significant both as an advance in basic knowledge, as well as a major advance in the use of large scale computing to solve complicated mathematical problems."
"This is an exciting breakthrough," said Prof Peter Sarnak at Princeton University. "Understanding and classifying the representations of E8 and Lie groups has been critical to understanding phenomena in many different areas of mathematics and science including algebra, geometry, number theory, physics and chemistry. This project will be invaluable for future mathematicians and scientists."
The ways that E8 manifests itself as a symmetry group are called representations. The goal is to describe all the possible representations of E8. These representations are extremely complicated, but mathematicians describe them in terms of basic building blocks. The new result is a complete list of these building blocks for the representations of E8, and a precise description of the relations between them, all encoded in a matrix, or grid, with 453,060 rows and columns. There are 205,263,363,600 entries in all, each a mathematical expression called a polynomial. If each entry was written in a one inch square, then the entire matrix would measure more than seven miles on each side.
The result of the E8 calculation, which contains all the information about E8 and its representations, is 60 gigabytes in size. This is enough to store 45 days of continuous music in MP3-format. If written out on paper, the answer would cover an area the size of Manhattan. The computation required sophisticated new mathematical techniques and computing power not available even a few years ago.
"This is an impressive achievement," said Hermann Nicolai, Director of the Albert Einstein Institute in Potsdam, Germany. "While mathematicians have known for a long time about the beauty and the uniqueness of E8, we physicists have come to appreciate its exceptional role only more recently - yet, in our attempts to unify gravity with the other fundamental forces into a consistent theory of quantum gravity, we now encounter it at almost every corner," he said, referring to efforts to combine the theory of the very big (general relativity) with the very small (quantum mechanics). "Thus, understanding the inner workings of E8 is not only a great advance for pure mathematics, but may also help physicists in their quest for a unified theory

No comments:
Post a Comment